DDP，全称Distributed Data Parallel，是一种数据并行的模型训练策略，尤其是在如今大模型盛行的时代，得到了广泛的使用。网络上有很多的文章介绍DDP，但大多都是通过流程、框架、别人的API调用示例为大家讲解。我看完之后也以为很简单，直到我自己从原理层面走完一遍，我才发现我并不真的懂。本文基于我个人的理解试图从更偏数学基础的角度讲清楚是DDP是怎么回事儿。（其实本人数学并不好，只是要把很多基础的东西讲清楚，目前水平有限，只能选择使用数学公式来表达。而且数学公式也会更严谨一些，自己想当然的一些错误也更容易规避一些。）

既然要介绍模型训练策略，就不得不回顾神经网络模型训练的基础过程。

1. 神经网络的前向与反向传播过程回顾

为了能够从数学公式上讲明白，我们定义一个简单的非典型的神经网络模型（其实更像是一个预测特定值的回归模型）。

这个神经网络模型的定义如下：

\[f(\mathbf x) = mean((\mathbf x \mathbf W)^3) \qquad (1)\]

其中

$\mathbf x \in \mathbb R^{B \times 2}$为神经网络的输入，$B$为batch size，$\mathbf x$本身的特征维度为2；
$\mathbf W \in \mathbb R^{2\times 1}$神经网络中的一个$2 \times 1$的线性变换所对应的参数。这是本神经网络中唯一的可训练参数。
由以上两点，可知$\mathbf x \mathbf W \in \mathbb R^{B \times 1}$；$(\mathbf x \mathbf W)^3$是一个element-wise的求立方的操作，因此$(\mathbf x \mathbf W)^3 \in \mathbb R^{B \times 1}$；$mean(\mathbf z)$表示对向量$\mathbf z$中的所有元素求平均值。所以，$mean((\mathbf x \mathbf W)^3) \in R^1$，即$f(\mathbf x)$最终的运算结果是一个一维的长度为1的向量。
显然$f(\mathbf x)$是一个连续的可导的函数，我们可以通过backward的过程，最终算出来$\frac{\partial f}{\partial \mathbf W}$的值。显然$\frac{\partial f}{\partial \mathbf W} \in \mathbb R ^{2 \times 1}$。

如果上面的数学符号不是很好理解，可以参考使用pytorch定义的跟$f(\mathbf x)$等价的神经网络：

import torch
import torch.nn as nn
class SimpleNet(nn.Module):
  def __init__(self):
    # 这里为了指定W的具体值，没有使用nn.Linear()之类的封装好的线性变换模块
    self.W = nn.Parameter(torch.tensor([[0.3],[0.4]]))
  def forward(self, x):
   	return torch.mean(torch.pow( x @ W, 3))

1.1 前向传播过程

为了更短更精确表达，后续使用英文forward来表达前向传播过程；使用backward表达后续传播过程。$f(\mathbf x)$的forward过程很简单，就是公式$(1)$的计算过程，其中$\mathbf x \mathbf W \in \mathbb R^{B \times 1}$是一个形状（Shape）和Batch Size $B$相关的矩阵，如果Batch Size更大，则$\mathbf x \mathbf W$中的元素也越多。也就是说forward的计算过程是一个跟输入数据的Batch Size有关的过程。

1.2 反向传播过程

那么问题来了，backward的过程是否也是一个跟Batch Size有关的过程呢？我们在之前的博客torch.autograd.backward的工作原理中介绍了一些相关内容，让我们再来简单回顾一下：

backward过程的本质是计算损失$l$ (在本文所举的例子中$l = f(\mathbf x)$)，对所有的输入参数的梯度，在本文的例子中，只有一个参数$\mathbf W$，即求$\frac{\partial l}{ \partial \mathbf W}$; 其中$l$是一个标量，那么显然$\frac{\partial l}{ \partial \mathbf W}$与$\mathbf W$具有相同的Shape
$\frac{\partial l}{\partial \mathbf W}$的计算遵循导数的链式求导法则，如果我们将公式$(1)$计算的中间过程展开，则有如下的中间计算结果：

\[\begin{align*} g(\mathbf x) &= \mathbf x \mathbf W \qquad\qquad (2) \\ t(\mathbf g) &= \mathbf g^3 \qquad\qquad (3) \qquad \#\text{对矩阵内的每一个元素单独求三次方} \\ m(\mathbf t) &= mean(\mathbf t) \qquad (4) \qquad \#\text{对矩阵}\mathbf x中所有元素求均值 \\ l &= m \qquad (5) \end{align*}\]

如果是标量求导，那么按照链式求导法则有类似：$ \frac{\partial l}{\partial \mathbf W} = \frac{\partial l}{ \partial m} \frac{\partial m}{ \partial \mathbf t} \frac{\partial \mathbf t}{\partial \mathbf g} \frac{\partial \mathbf g}{ \partial \mathbf W}$ （中学课本里的链式求导法则，这里只是示意，并不代表精准计算过程，实际计算请以下面的推导出的等式（6）为准）的形式。但我们这里是对向量求导。假设我们有一个向量$\mathbf u = s(\mathbf v)$，其中$s(\cdot)$是一个函数；$\mathbf u \in \mathbb R^M$, $\mathbf v \in \mathbb R^N$，那么我们求$\mathbf u$对$\mathbf v$的导数，实际上会形成一个Jacobian矩阵：

\[\frac{\partial \mathbf u}{\partial \mathbf v} = \begin{bmatrix} \frac{\partial u_1}{\partial v_1} & \frac{\partial u_1}{\partial v_2} & \cdots \frac{\partial u_1}{\partial v_N} \\ \frac{\partial u_2}{\partial v_1} & \frac{\partial u_2}{\partial v_2} & \cdots \frac{\partial u_2}{\partial v_N} \\ \vdots \\ \frac{\partial u_M}{\partial v_1} & \frac{\partial u_M}{\partial v_2} & \cdots \frac{\partial u_M}{\partial v_N} \\ \end{bmatrix} \in \mathbb R^{M \times N}\]

我们在下文中，都是使用这种Jacobian矩阵来表达向量之间的导数。

根据公式$(2),(3),(4),(5)$以及Jacobian矩阵的定义，我们可以得到如下的导数计算公式

\[\begin{align*} \frac{\partial l}{\partial m} &= 1 \\ \frac{\partial m}{\partial \mathbf t} &= \begin{bmatrix} \frac{\partial m}{\partial t_1} & \frac{\partial m}{\partial t_2} & \cdots & \frac{\partial m}{\partial t_B} \end{bmatrix} = \begin{bmatrix} \frac{1}{B} & \frac{1}{B} & \cdots & \frac{1}{B} \end{bmatrix} \\ \frac{\partial \mathbf t}{ \partial \mathbf g} &= \begin{bmatrix} \frac{\partial t_1}{\partial g_1} & \frac{\partial t_1}{\partial g_2} & \cdots & \frac{\partial t_1}{\partial g_B} \\ \frac{\partial t_2}{\partial g_1} & \frac{\partial t_2}{\partial g_2} & \cdots & \frac{\partial t_2}{\partial g_B} \\ \vdots \\ \frac{\partial t_B}{\partial g_1} & \frac{\partial t_B}{\partial g_2} & \cdots & \frac{\partial t_B}{\partial g_B} \end{bmatrix} = \begin{bmatrix} 3g_1^2 & 0 & 0 &\cdots & 0 \\ 0 & 3g_2^2 & 0 & \cdots & 0 \\ \vdots \\ 0 & 0 & \cdots & 0 & 3g_B^2 \end{bmatrix} \\ \frac{\partial \mathbf g}{\partial \mathbf W} &= \begin{bmatrix} \frac{\partial g_1}{\partial W_1} & \frac{\partial g_1}{\partial W_2} \\ \frac{\partial g_2}{\partial W_1} & \frac{\partial g_2}{\partial W_2} \\ \vdots \\ \frac{\partial g_B}{\partial W_1} & \frac{\partial g_B}{\partial W_2} \end{bmatrix} = \begin{bmatrix} x_{1,1} & x_{1,2} \\ x_{2,1} & x_{2,2} \\ \vdots \\ x_{B,1} & x_{B,2} \end{bmatrix} \end{align*} \qquad (5)\]

如果按照严格的Jocobian矩阵相乘，实际上

\[\frac{\partial l}{\partial \mathbf W} = \left( \frac{\partial \mathbf g}{ \partial \mathbf W} \right)^\top \left( \left(\frac{\partial \mathbf t}{ \partial \mathbf g} \right)^\top \frac{\partial m}{\partial \mathbf t} \right ) \qquad (6)\]

所以这里的答案是，backward同样也是一个跟输入数据高度相关的相关的过程（因为backward过程中用到了输入的每一个数据$x_{i,j}$ ，其中$i \in {1,2…B}$，$j \in { 1,2 }$）。公式$(6)$实际上从矩阵计算的顺序上来看，也很好的反映出”反向传播”这一概念。

2. DDP的宏观概念

讨论清楚forward以及backward的计算过程之后，我们终于可以回到DDP上，什么是DDP？（本文将跳过DP的介绍，直接介绍DDP）。从宏观上来说DDP属于使一种叫做SPMD的编程范式，SPMD并不是一个数学概念，而是目前DDP实现中被广泛采用的一种编程模型；

SPMD的全称是Single Program Multiple Data。理解这种编程范式，对于我们理解模型训练的过程，以及debugging，写自己的并行训练框架都有很大的好处。下图是一个典型的SPMD计算的场景，Process #k(k=1…N)执行同一段代码，且处理不同的输入Input #k；不同的Process #i与Process #j 且$j \ne i$之间会进行Collective communication（每一个Process #k原则上都需要执行同一个通信原语（如图中黄色框中所示），关于什么是Collective communication后面介绍）

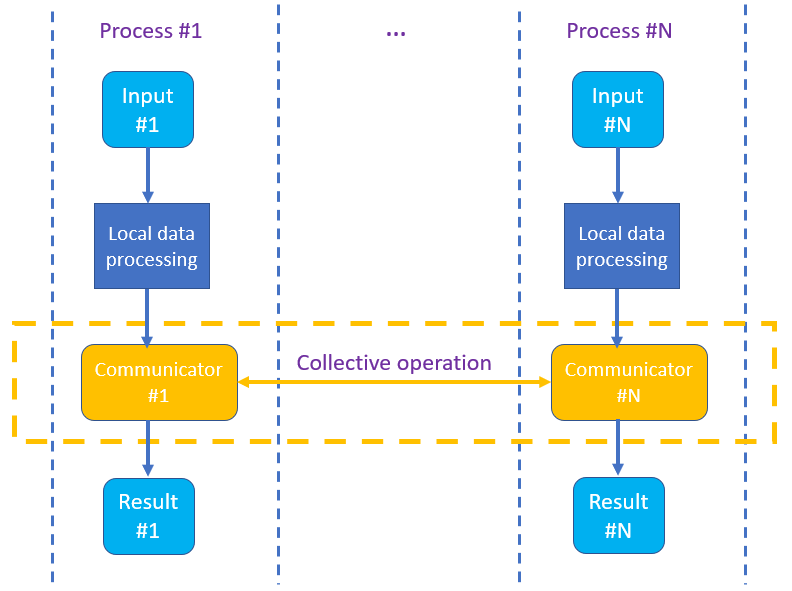
spmd_flow

让SPMD工作的关键是基于MPI（Message Passing Interface）消息通信。以上的截图很生动地表达了是SPMD的工作过程，那么我们如何在我们刚讨论的神经网络上实现DDP呢？

2.1 DDP的数学概念

假设有一批数据$D$，其中样本数为$B$，$D$本来是用在一次batch训练中的数据。但因为$D$很大，我们没有这么大内存的机器，所以我们把这批数据$\mathbf x$分为两份$D_i$($i = 1,2$) ，其中$D_i$含有的样本数量为$B_i$ ，那么$B = B_1 + B_2$。

考虑以下两种情况：

情况一：

我们有一天发财了，有一台内存（或显存）足够大的机器$M_D$，在forward过程中，可以设定batch size为$B$，因此，可以一次使用数据$D$，执行forward以及backward过程，按照我们之前的讨论，backward过程可计算出神经网络中，所有叶节点参数的梯度：$\lbrace \text{grad}_{w_k}^D \mid w_k是神经网络的中任意参数 \rbrace $）

情况二:

我们有两台机器$M_{D_1}$以及$M_{D_2}$，其分别使用数据$D_1$，$D_2$基于神经网络(1)，运行foward，以及backward过程；在$M_{D_i}$上产生叶节点参数的梯度: $\lbrace \text{grad}_{w_k}^{D_i} \mid w_k是神经网络中的任意参数,且i=1或2 \rbrace $。

所谓DDP，实际上就是，我们希望在机器$M_{D_i}$进行完各自的backward之后，通过数据交换$ \lbrace grad_{w_k}^{D_i} \mid w_k是神经网络中的任意参数 \rbrace $，获取到$ \lbrace grad_{w_k}^{D_{ i \% 2 + 1} } \mid w_k是神经网络中的任意参数 \rbrace $，且通过函数$f(\cdot)$使得，在机器$M_{D_i}$上，实现 $ grad_{w_k}^{D} = f( grad_{w_k}^{ D_i}, grad_{w_k}^{D_{i \% 2 + 1}}) $，从而在$M_{D_i}$上各自独立更新神经网络参数且始终保持$M_{D_1}$以及$M_{D_2}$上具有完全相同的神经网络参数；

用大白话来描述，就是机器$M_{D_1}$和$M_{D_2}$完成各自的backward过程之后，彼此交换使用$D_1$和$D_2$计算出来的$ grad_{w_k}^{D_1} $和$ grad_{w_k}^{D_2} $，使得$M_{D_1}$和$M_{D_2}$这两台机器上都有彼此的梯度数据，即都有：$\lbrace grad_{w_k}^{D_1}, grad_{w_k}^{D_2} \rbrace $，然后通过一个函数$f(\cdot)$使得在两个机器上，各自独立恢复出$ grad^D_{w_k} $。从而实现即使我们没有内存足够大的机器$M_D$，也能够在两台（甚至多台）机器$M_{D_1}$，$M_{D_2}$等效实现一次性处理一大批数据$D$的效果。

所以，现在的关键是，我们要能够找出一个函数$f(\cdot)$，使得$ grad_{w_k}^D = f(grad_{w_k}^{D_1}, grad_{w_k}^{D_2})$

2.2 反向传播过程的分块矩阵表达

如果我们将公式$(5)$中的除了$\frac{\partial l}{ \partial m}$之外的所有Jacobian矩阵写成分块儿矩阵的形式（按照$B=B_1 + B_2$进行拆分两个部分），如下所示：

\[\begin{align*} \frac{\partial l}{\partial m} &= 1 \\ \frac{\partial m}{\partial \mathbf t} &= \begin{bmatrix} \left ( \frac{\partial m}{ \partial t_{1...B_1}} \right )^\top \\ \left ( \frac{\partial m}{ \partial t_{B_1+1...B}} \right )^\top \end{bmatrix} \in \mathbb R^{B \times 1} \qquad \#按照Jacobian函数，\frac{\partial m}{ \partial t_{1...B_1}}是一个1\times B_1的矩阵，所以使用转置，使其变成为一个B_1 \times 1的矩阵块 \\ \frac{\partial \mathbf t}{ \partial \mathbf g} &= \begin{bmatrix} \frac{\partial t_{1...B_1}}{\partial g_{1...B_1}} & \frac{\partial t_{1...B_1}}{\partial g_{B_1+1...B}} \\ \frac{\partial t_{B_1+1...B}}{\partial g_{1...B_1}} & \frac{\partial t_{B_1+1...B} }{ \partial g_{B_1+1...B}} \end{bmatrix} = \begin{bmatrix} \frac{\partial t_{1...B_1}}{\partial g_{1...B_1}} & \mathbf 0^{B_1 \times B_2} \\ \mathbf 0^{B_2 \times B_1} & \frac{\partial t_{B_1+1...B} }{ \partial g_{B_1+1...B}} \end{bmatrix} \in \mathbb R^{B \times B} \qquad \#\mathbf 0^{m \times n}表示一个m\times n的全0矩阵； \\ \frac{\partial \mathbf g}{ \partial \mathbf W} &= \begin{bmatrix} \frac{\partial g_{1...B_1}}{w_{1...2}} \\ \frac{\partial g_{B_1+1...B}}{w_{1...2}} \end{bmatrix} \in \mathbb R^{B \times 2} \end{align*} \qquad (7)\]

其中$\frac{\partial t_{r_i…r_j}}{\partial g_{c_k…c_p}}$表示一个表示原Jacobian矩阵中，行范围从$r_i$到$r_j$，列范围从$c_k$到$c_p$的一个矩阵分块；其他类似表达,意思相近；此处不再赘述；

我们将公式$(7)$(公式太长，标号$(7)$可能需要拉滚动条才能看到)中的各项，代入到公式$(6)$中，重新计算$\frac{\partial l}{ \partial \mathbf W}$有：

\[\begin{align*} \frac{\partial l}{\partial \mathbf W} &= \left( \frac{\partial \mathbf g}{ \partial \mathbf W} \right)^\top \left( \left(\frac{\partial \mathbf t}{ \partial \mathbf g} \right )^\top \frac{\partial m}{\partial \mathbf t} \right ) \qquad \#原公式(6) \\ &= \begin{bmatrix} \frac{\partial g_{1...B_1}}{w_{1...2}} \\ \frac{\partial g_{B_1+1...B}}{w_{1...2}} \end{bmatrix} ^\top \left ( \begin{bmatrix} \frac{\partial t_{1...B_1}}{\partial g_{1...B_1}} & \mathbf 0^{B_1 \times B_2} \\ \mathbf 0^{B_2 \times B_1} & \frac{\partial t_{B_1+1...B} }{ \partial g_{B_1+1...B}} \end{bmatrix}^\top \begin{bmatrix} \left ( \frac{\partial m}{ \partial t_{1...B_1}} \right )^\top \\ \left ( \frac{\partial m}{ \partial t_{B_1+1...B}} \right)^\top \end{bmatrix} \right ) \qquad \#将公式(7)中的各部分代入进来 \\ &= \begin{bmatrix} \frac{\partial g_{1...B_1}}{w_{1...2}} \\ \frac{\partial g_{B_1+1...B}}{w_{1...2}} \end{bmatrix} ^\top \left ( \begin{bmatrix} (\frac{\partial t_{1...B_1}}{\partial g_{1...B_1}})^\top & \mathbf 0^{B_1 \times B_2} \\ \mathbf 0^{B_2 \times B_1} & (\frac{\partial t_{B_1+1...B} }{ \partial g_{B_1+1...B}})^\top \end{bmatrix} \begin{bmatrix} \left ( \frac{\partial m}{ \partial t_{1...B_1}} \right )^\top \\ \left ( \frac{\partial m}{ \partial t_{B_1+1...B}} \right )^\top \end{bmatrix} \right ) \qquad \#将公式上一步中第二个矩阵进行转置，因分块矩阵满足 \begin{bmatrix} A & B \\ C & D \end{bmatrix}^\top = \begin{bmatrix} A^\top & C^\top \\ B^\top & D^\top \end{bmatrix} \\ &= \begin{bmatrix} \frac{\partial g_{1...B_1}}{w_{1...2}} \\ \frac{\partial g_{B_1+1...B}}{w_{1...2}} \end{bmatrix}^\top \begin{bmatrix} \left(\frac{\partial t_{1...B_1}}{\partial g_{1...B_1}} \right)^\top \left ( \frac{\partial m}{ \partial t_{1...B_1}} \right )^\top \\ (\frac{\partial t_{B_1+1...B} }{ \partial g_{B_1+1...B}})^\top \left ( \frac{\partial m}{ \partial t_{B_1+1...B}} \right)^\top \end{bmatrix} \qquad \#上一步括号中的矩阵相乘 \\ &= \begin{bmatrix} \left(\frac{\partial g_{1...B_1}}{w_{1...2}} \right)^\top & \left(\frac{\partial g_{B_1+1...B}}{w_{1...2}} \right)^\top \end{bmatrix} \begin{bmatrix} \left(\frac{\partial t_{1...B_1}}{\partial g_{1...B_1}} \right)^\top \left ( \frac{\partial m}{ \partial t_{1...B_1}} \right )^\top \\ (\frac{\partial t_{B_1+1...B} }{ \partial g_{B_1+1...B}})^\top \left ( \frac{\partial m}{ \partial t_{B_1+1...B}} \right)^\top \end{bmatrix} \qquad \#第一个矩阵进行转置 \\ &= \left(\frac{\partial g_{1...B_1}}{w_{1...2}} \right)^\top \left(\frac{\partial t_{1...B_1}}{\partial g_{1...B_1}} \right)^\top \left ( \frac{\partial m}{ \partial t_{1...B_1}} \right )^\top + \left(\frac{\partial g_{B_1+1...B}}{w_{1...2}} \right)^\top \left(\frac{\partial t_{B_1+1...B} }{ \partial g_{B_1+1...B}}\right)^\top \left ( \frac{\partial m}{ \partial t_{B_1+1...B}} \right)^\top \end{align*} \qquad (8)\]

在我们的设定中，$m = l$，所以我们也可以将上面的公式$(8)$（标号需拉滚动条才能看到）写作：

\[\frac{\partial l}{\partial \mathbf W} = \left(\frac{\partial g_{1...B_1}}{w_{1...2}} \right)^\top \left(\frac{\partial t_{1...B_1}}{\partial g_{1...B_1}} \right)^\top \left ( \frac{\partial l}{ \partial t_{1...B_1}} \right )^\top + \left(\frac{\partial g_{B_1+1...B}}{w_{1...2}} \right)^\top \left(\frac{\partial t_{B_1+1...B} }{ \partial g_{B_1+1...B}}\right)^\top \left ( \frac{\partial l}{ \partial t_{B_1+1...B}} \right )^\top \qquad (9)\]

如果数据$D_1$和$D_2$分别在机器$M_{D_1}$以及$M_{D_2}$上运行，分别产生loss值$l_1$和$l_2$，那么在$M_{D_1}$以及$M_{D_2}$上，我们分别有

\[\begin{align*} \frac{\partial l_1}{\partial \mathbf W} &= \left(\frac{\partial g_{1...B_1}}{w_{1...2}} \right)^\top \left(\frac{\partial t_{1...B_1}}{\partial g_{1...B_1}} \right)^\top \left ( \frac{\partial l_1}{ \partial t_{1...B_1}} \right )^\top \qquad (10) \\ \frac{\partial l_2}{\partial \mathbf W} &= \left(\frac{\partial g_{B_1+1...B}}{w_{1...2}} \right)^\top \left(\frac{\partial t_{B_1+1...B} }{ \partial g_{B_1+1...B}}\right)^\top \left ( \frac{\partial l_2}{ \partial t_{B_1+1...B}} \right )^\top \qquad (11) \end{align*}\]

注意到在公式$(5)$我们已经有了$\frac{\partial l}{ \partial \mathbf t}$（即$\frac{\partial m}{\partial \mathbf t}$）的取值，这是针对数据$D$的，那么

\[\begin{align*} \left( \frac{\partial l_1}{ \partial t_{1...B1}} \right)^\top &= \begin{bmatrix} \frac{\partial l_1}{\partial t_1} \\ \frac{\partial l_1}{\partial t_2} \\ \vdots \\ \frac{\partial l_1}{\partial t_{B_1}} \end{bmatrix} = \begin{bmatrix} \frac{1}{B_1} \\ \frac{1}{B_1} \\ \vdots \\ \frac{1}{B_1} \end{bmatrix} \\ \left( \frac{\partial l_2}{ \partial t_{B_1+1...B}} \right)^\top &= \begin{bmatrix} \frac{\partial l_2}{\partial t_{B_1+1}} \\ \frac{\partial l_2}{\partial t_{B_1+2}} \\ \vdots \\ \frac{\partial l_2}{\partial t_{B}} \end{bmatrix} = \begin{bmatrix} \frac{1}{B_2} \\ \frac{1}{B_2} \\ \vdots \\ \frac{1}{B_2} \end{bmatrix} \end{align*} \qquad (12)\]

根据公式$(9),(10),(11),(12)$我们可以看出来，$\frac{\partial l}{ \partial \mathbf W}$ 与 $\frac{\partial l_1}{\partial \mathbf W} $以及$\frac{\partial l_2}{\partial \mathbf W}$有如下的关系：

\[\frac{\partial l}{\partial \mathbf W} = \frac{B_1}{B} \frac{\partial l_1}{ \partial \mathbf W} + \frac{B_2}{B} \frac{\partial l_2}{\partial \mathbf W}\]

即，我们终于找到了我们所要寻找的函数$f(\cdot)$，$f(grad_{w_k}^{D_1}, grad_{w_k}^{D_2}) = \frac{B1}{B} grad_{w_k}^{D_1} + \frac{B_2}{B} grad_{w_k}^{D_2}$

我们进一步扩展，如果将数据$D$分为$K$份，且$D_i$在机器$M_{D_i}$上运行foward以及backward过程；那么要获得与单一机器运行$D$的等价的梯度数据，可以通过以下的方式来计算（其中$\mathbf W$是网络中的任意一个参数）：

\[\frac{\partial l}{\partial \mathbf W} = \sum_{i=1}^K \frac{B_i}{B} \frac{\partial l_i}{ \partial \mathbf W} \qquad (13)\]

我们注意到我们在这个简单的网络中，最终使用了$mean(\cdot)$作为对于$B$个loss值到单一标量值的规约。所以才使得我们有了公式$(13)$这种形式，如果我们将这个$mean(\cdot)$替换成$sum(\cdot)$呢？又或者是$max(\cdot),min(\cdot)$呢？显然最终起影响作用的，都是这个规约函数的选择；读者可自行验证各种规约函数。

2.3 DDP代码实现

最后一部分，我们来真正介绍DDP的代码实现过程；显然我们只需要每个机器$M_{D_i}$在执行完各自单独的backward操作之后，执行一个all-gather的动作，然后再运行我们之前定义的函数$f(\cdot)$，例如公式$(13)$。

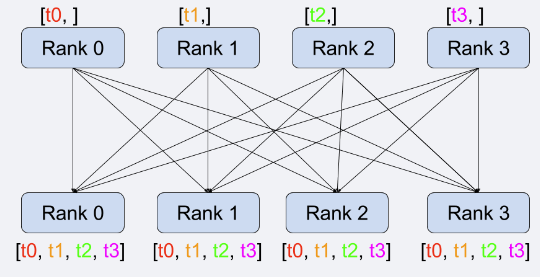
上图展示了一个典型的all_gather的操作。每一个Rank代表了一个执行的训练的进程。假设每一个Rank执行完各自的backward操作之后，所产生的局部梯度数据为$t_i$（如上图），然后所有$\text{Rank}_i$都执行all_gather操作，这样每一个$\text{Rank}_i$最终都会拥有其他Rank的梯度数据。然后他们使用我们定义的$f(\cdot)$函数，恢复出完整的梯度数据。然后使用设定的学习率$\eta$ 来进行参数的更新。

参考文献：

Distributed communication package - torch.distributed
Single Program Multiple Data
https://pytorch.org/tutorials/intermediate/dist_tuto.html